How Meilisearch updates a database with millions of vector embeddings in under a minute

This is part 4 of a series of blog posts originally published on Clément Renault's blog. Begin the journey with part 1, part 2, and part 3. This blog post considers that you’ve already read parts 1 and 2.

In this blog post, we’ll talk about how we implemented incremental indexing in Arroy. By incremental, we mean that when inserting or deleting items in a tree, we can update only the required parts instead of rebuilding everything.

At Meilisearch, that’s essential because our users usually send updates regularly, and their content constantly changes. Rebuilding everything from scratch is very costly and won’t give a good experience; that’s why we already spent a lot of time on our latest release to make all the data structures support incremental indexing and arroy being one of them, we HAD TO implement it as well!

The theory

The following schema shows a high-level view of what should happen when adding and deleting documents into an existing tree.

As a reminder, arroy is a vector store based on LMDB, an embedded transactional memory-mapped key-value store. It stores your vectors in trees composed of three kinds of nodes:

• The split nodes - Store information on which item IDs are spread out between its left and right.
• The descendants' nodes - Store multiple item IDs.
• The items - A single vector.

For the following examples, we’ll consider the descendants node cannot contain more than two items and that the closer the IDs are, the closer the items are in space. For example, the item 1 is close to the item 2 but is farther from the item 10.

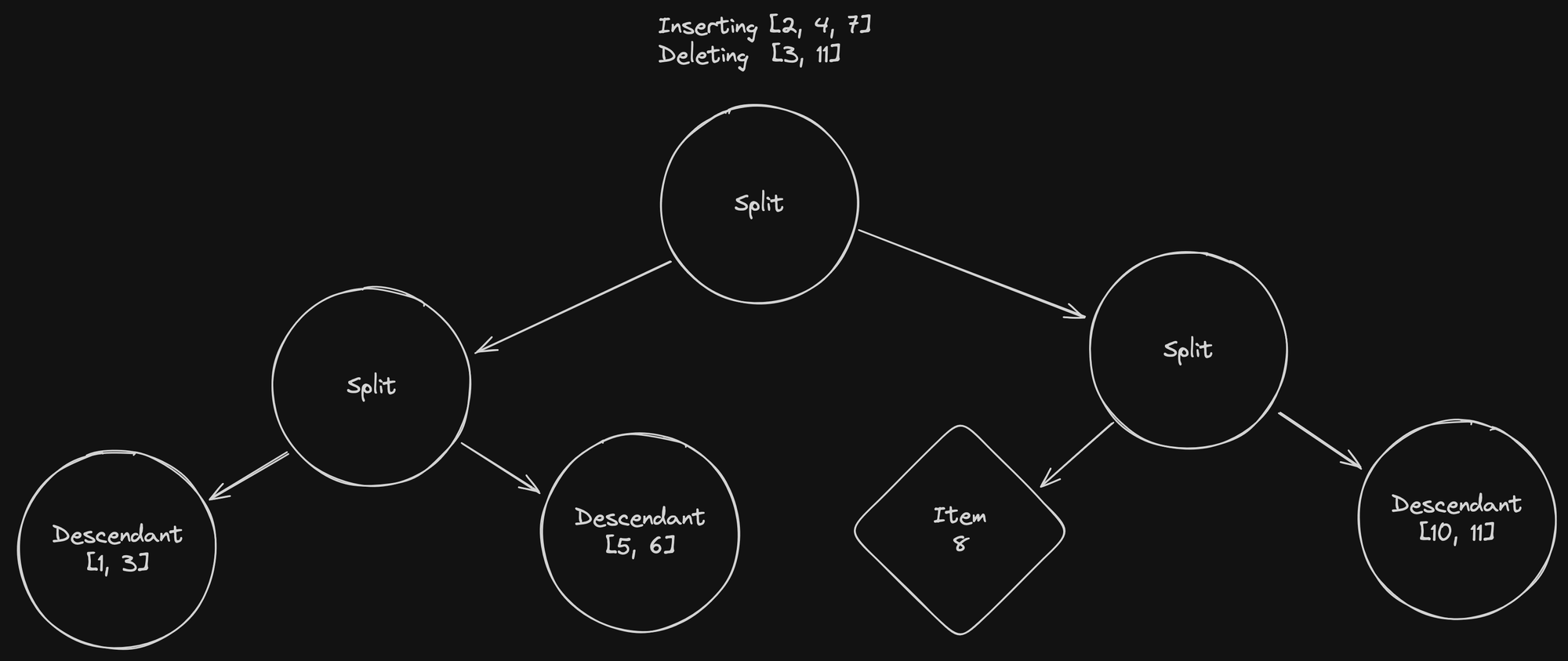
Here, we’re trying to insert items 2 and 7 and delete items 3 and 11.

Following what we do on the search, we split the items to insert between the left and right split nodes. But the deleted items are no longer present in the database! We don't have their associated vector, and therefore we'll need to iterate over all the leaves to find and delete them.

Fortunately, since we use roaring bitmaps, this list doesn't consume much memory, and since we never update it, we can share it with every thread without ever copying it 🎉

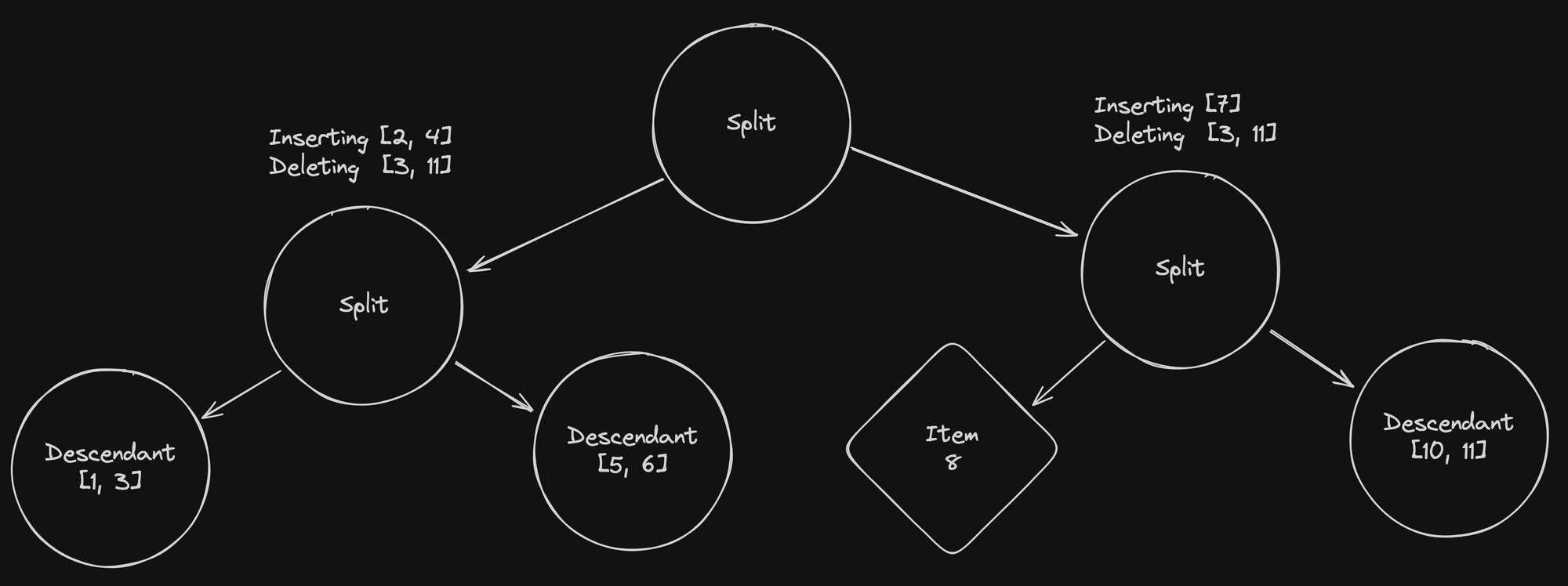
Notice how the items to insert were balanced between the left and right split nodes. In the next step, we’ll follow the same process and split both lists of items to insert on the split node.

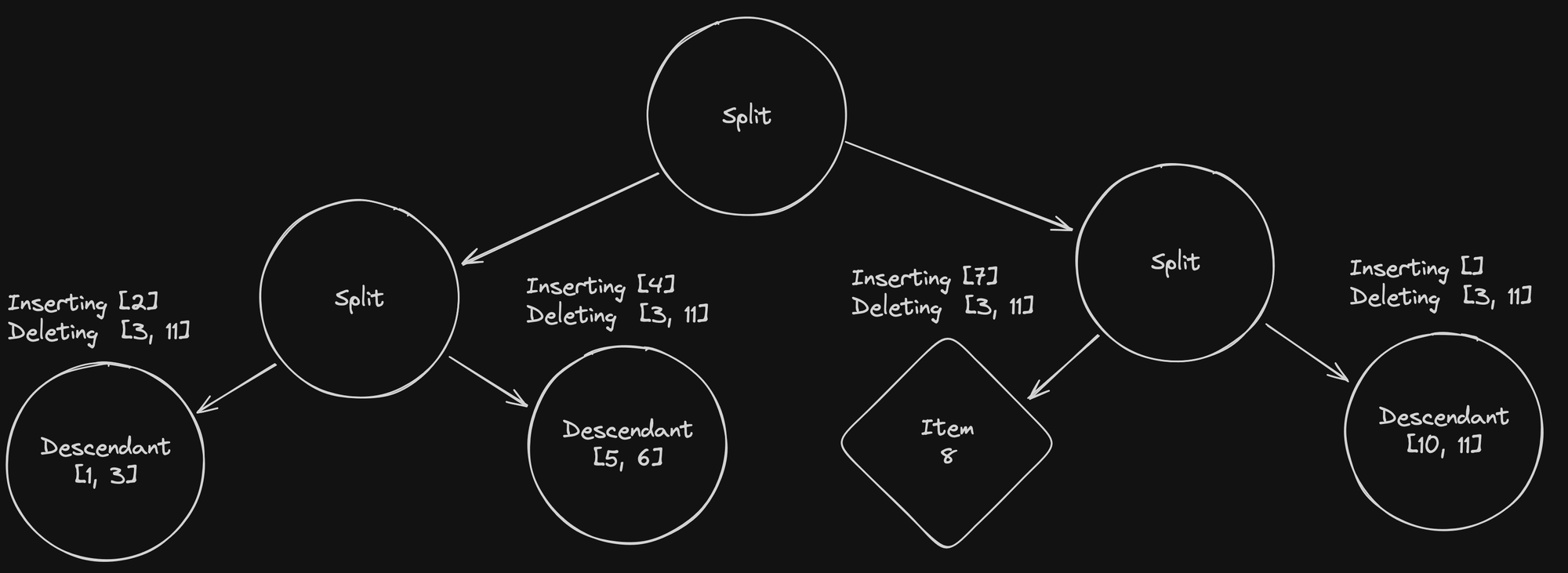
It’s on this step that all the good stuff happens. From the left to the right:

• The first descendant node gets its item 3 removed, and item 2 added.
• The second descendant node gets too big and must be replaced by a new split node.
• The item 8 becomes a descendant containing both the items 7 and 8.
• After deleting item 10 in the last descendant node, we replace it with a direct link to an item to reduce the number of nodes in the tree (and improve search time by reducing the number of lookups).

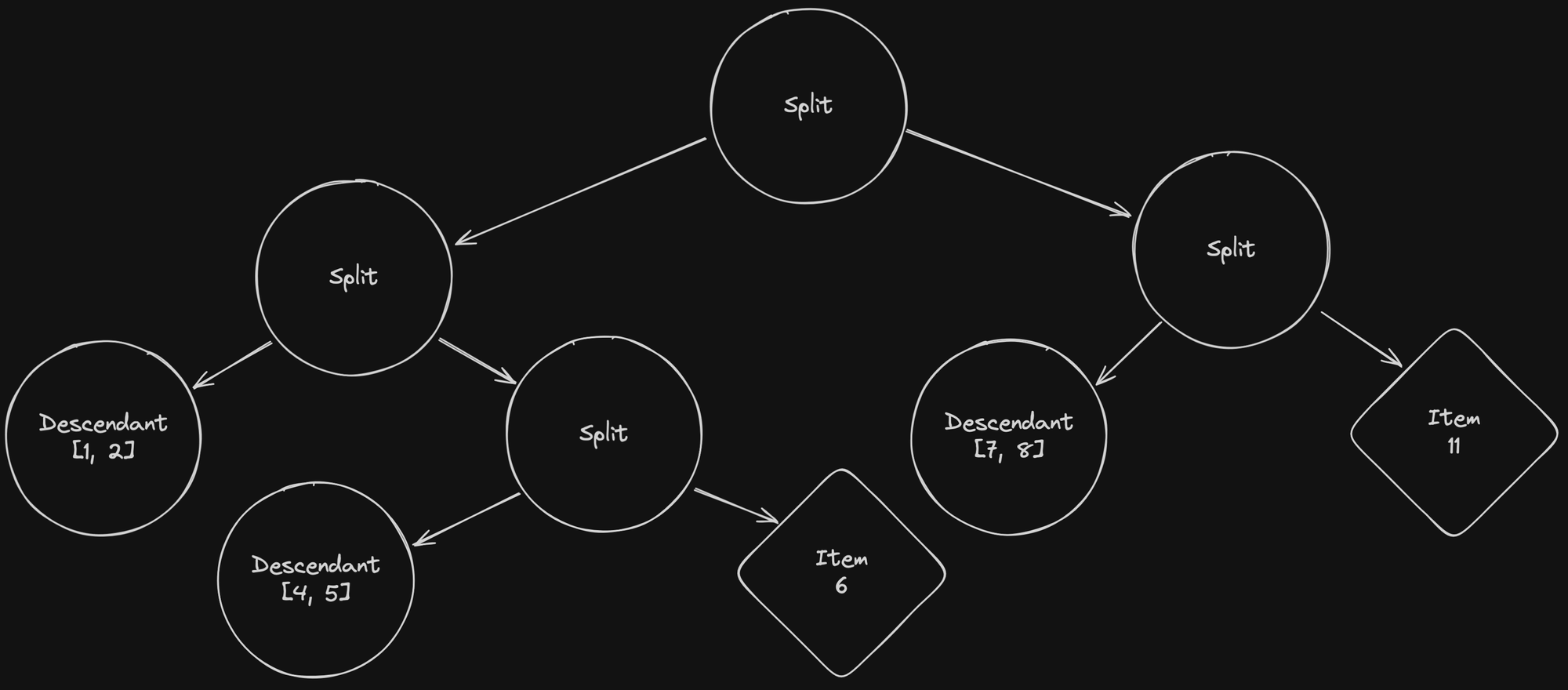
Now that you’ve seen all the steps of our incremental indexing process, we’re still going to take a few notes on what happened:

• In the first three steps, we had to read all of the tree nodes, which, by default, is equal to the total number of items in the database.
• In the last step, we had to write four new tree nodes. Previously we would have rewritten the whole tree. The number of writes, which is the slowest operation in databases, is reduced to the bare minimum.
• The process works on a single tree which means we can still multi-thread the computation of every tree.
• The IDs aren’t sequential anymore, which doesn't play well with the ID generation strategy described in Writing the tree in parallel.

How did we fix the ID generation?

At the start of the indexing process, we need to gather all the existing tree IDs.
The information we need to generate new nodes are:

• The total number of tree nodes used to know when to stop building trees.
• The « holes » in the used IDs that we want to re-use. This fragmentation is produced when we edit the trees.
• The highest ID existing in the trees to generate the next new IDs.

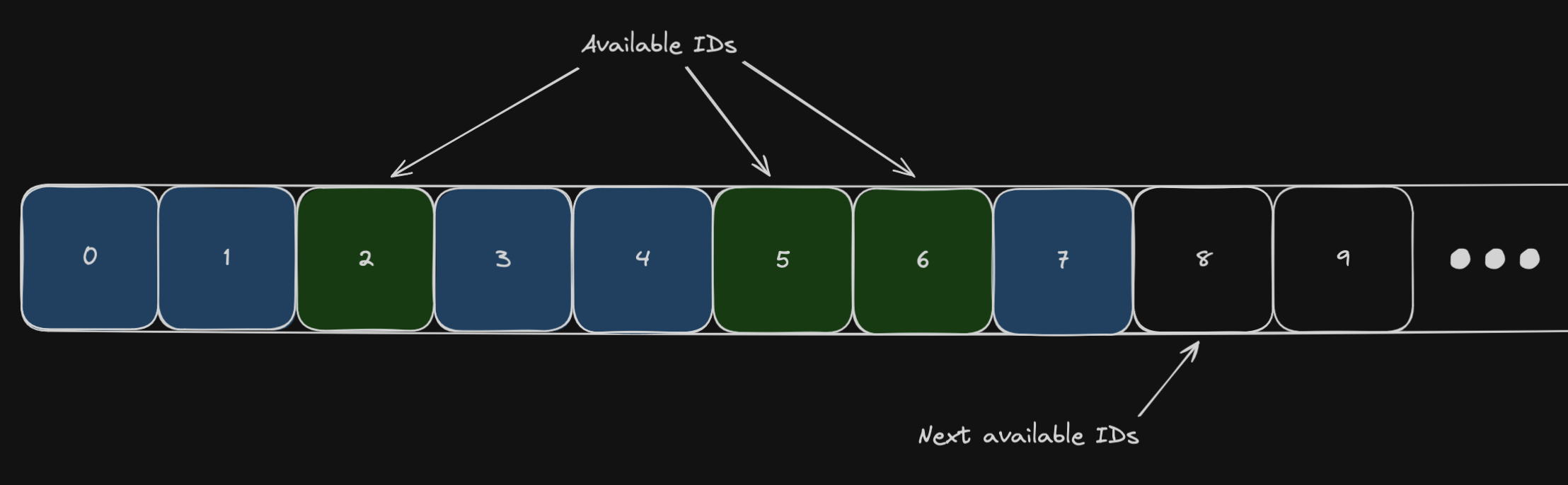
The « simple » idea is to have a counter for the total number of tree nodes. A counter that we can increment to generate new fresh IDs. The most challenging part is to pick an available ID shared between threads and without big mutexes.

It took me quite some time to find a solution for this last point; I implemented a whole complex solution (150loc) that I ended up rewriting entirely from scratch in one hour for an easy and more efficient solution. We're going to see all the ideas we went through before finding our final solution.

Sharing an iterator over the available IDs

The first and most straightforward idea that comes to mind is to create and share an iterator over all the available IDs.

let mut available_ids = available_ids.into_iter();

roots.into_par_iter().for_each(|root| {
    // stuff
    let next_id = available_ids.next();
    // stuff
});

If you’re familiar with Rust, you’ll notice immediately that the for_each cannot capture a mutable reference over the available_ids because we use the into_par_iter method from Rayon that execute the next methods on the iterator in a multi-threaded way. Which means we can't call .next().

By using a mutex (short for mutual exclusion), we can make it compile:

let mut available_ids = Mutex::new(available_ids.into_iter());

roots.into_par_iter().for_each(|root| {
    // stuff
    let next_id = available_ids.lock().unwrap().next();
    // stuff
});

That is safe and will yield the right results, but won’t scale well as all the threads have to wait for each other on the lock.

Let each thread own its list of IDs

When you need to remove a lock, a common solution is to split the work beforehand so each thread can work to its full capacity without ever having to know what’s happening on the other threads. That’s the solution I implemented initially. The idea is to explode the roaring bitmap into as many smaller roaring bitmaps as there are trees to update.

The following function can split a roaring bitmap into n sub-bitmaps of equal size:

pub fn split_ids_in(available: RoaringBitmap, n: usize) -> Vec<RoaringBitmap> {
    // Define the number of elements per sub-bitmap
    let chunk_size = available.len() / n as u64;
    let mut ret = Vec::new();

    let mut iter = available.into_iter();
    for _ in 0..(n - 1) {
        // Create a roaring bitmap of `chunk_size` elements from the iterator without consuming it
        let available: RoaringBitmap = iter.by_ref().take(chunk_size as usize).collect();
        ret.push(available);
    }
    // the last element is going to contain everything remaining
    ret.extend(iter);

    ret
}

With this function available, it's then trivial to use one bitmap per tree to update with the zip method on the parallel iterators of Rayon:

let available_ids = split_ids_in(available_ids, roots.len());

roots.into_par_iter().zip(available_ids).for_each(|(root, available_ids)| {
    let mut available_ids = available_ids.into_iter();
    // stuff
    let next_id = available_ids.next();
    // Here, we can use the available_ids without any locks or inter-thread synchronization
    // stuff
});

This works well while we're updating the already existing root trees. But later on, we may want to create new trees from scratch, and we can't know in advance how many new trees we’ll need to create. That's an issue because, without this information, we don't know how many sub-bitmaps we need to create.

At this point, I couldn’t see an easy fix to this problem, but I made the assumption that we rarely create a lot of new trees and that all new trees would use a lot of IDs. This means, giving all the IDs to the first new tree would probably work out (it’s hard to be 100% sure without monitoring it in prod).

The final solution

The previous solution was complex and did not even work perfectly. While I was scrolling through the documentation of the Roaring Bitmap, I saw the select method and immediately understood how I could make the initial approach works.

This method lets you get the values in your bitmap by index in an efficient way.
For example, with the following values in a bitmap: 13, 14, 15, 98, 99, 100:

• select(0) returns 13.
• select(3) returns 98.
• select(5) returns 100.
• select(6) returns None.

With that in mind, if we share the bitmap with all threads in read-only and share the index in the bitmap as an atomic number, we can have multiple threads get available IDs at the same time with lock-free synchronization.

Once the select method returns None, it means we can stop picking IDs from the bitmap and instead simply generate new IDs from scratch with the old method.
Even if it's super fast, calling the select method still takes some time, so once a thread gets a None returned from the method, we're going to update an atomic boolean telling us if there are still values to look at in the bitmap. If not, we can skip calling select and directly generate a new ID.

With that in mind, the cool ConcurrentNodeIds structure we showed you before in part 2 got a little bit more complex but it still let us generate IDs fairly without any locks!

/// A concurrent ID generator that will never return the same ID twice.
pub struct ConcurrentNodeIds {
    /// The current tree node ID we should use if no other IDs are available.
    current: AtomicU32,
    /// The total number of tree node IDs used.
    used: AtomicU64,

    /// A list of IDs to exhaust before picking IDs from `current`.
    available: RoaringBitmap,
    /// The current Nth ID to select in the bitmap.
    select_in_bitmap: AtomicU32,
    /// Tells if you should look in the roaring bitmap or if all the IDs are already exhausted.
    look_into_bitmap: AtomicBool,
}

impl ConcurrentNodeIds {
    /// Creates an ID generator returning unique IDs, avoiding the specified used IDs.
    pub fn new(used: RoaringBitmap) -> ConcurrentNodeIds {
        let last_id = used.max().map_or(0, |id| id + 1);
        let used_ids = used.len();
        let available = RoaringBitmap::from_sorted_iter(0..last_id).unwrap() - used;

        ConcurrentNodeIds {
            current: AtomicU32::new(last_id),
            used: AtomicU64::new(used_ids),
            select_in_bitmap: AtomicU32::new(0),
            look_into_bitmap: AtomicBool::new(!available.is_empty()),
            available,
        }
    }

    /// Returns a new unique ID and increases the count of IDs used.
    pub fn next(&self) -> Result<u32> {
        if self.look_into_bitmap.load(Ordering::Relaxed) {
            let current = self.select_in_bitmap.fetch_add(1, Ordering::Relaxed);
            match self.available.select(current) {
                Some(id) => Ok(id),
                None => {
                    self.look_into_bitmap.store(false, Ordering::Relaxed);
                    Ok(self.current.fetch_add(1, Ordering::Relaxed))
                }
            }
        } else {
            Ok(self.current.fetch_add(1, Ordering::Relaxed))
        }
    }
}

Performances in practice

I haven’t run a lot of benchmarks yet (I would like to, though, and may update this post later), but on my benchmarks with a few hundred thousand items, here are the results I get:

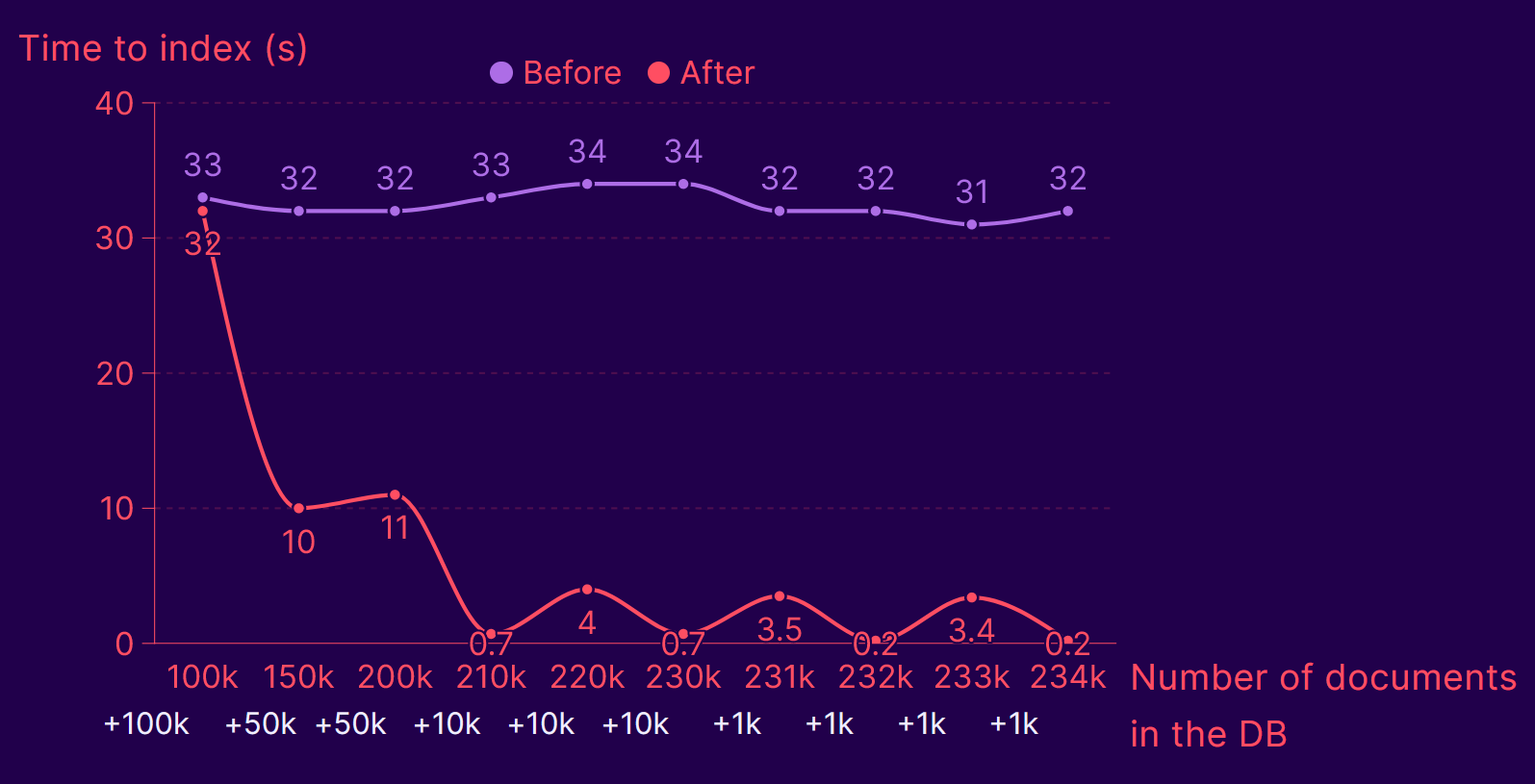
• On average, we get more than a 10x speedup after three batches of items indexed.
• The little bumps we observe afterward that make us go from ~700ms to ~3s are due to the creation of new trees as the number of items increases.
• I expect this benchmark to represent a worst-case scenario:
  • All my item IDs are randomly generated, which means there are very few duplicates/updates but always new insertions and more writing.
  • My vectors are also randomly generated with a uniform distribution, which means there shouldn’t be clusters as we observe in a real-life dataset.

This feature is now being used on production data with millions of documents, and we've seen numbers in the range of 9000 items added on a 2M items database in under a minute.

Meilisearch is an open-source search engine enabling developers to build state-of-the-art experiences while enjoying simple, intuitive DX. 

For more things Meilisearch, you can join the community on Discord or subscribe to the newsletter. You can learn more about the product by checking out the roadmap and participating in product discussions.